0 初衷
很多介绍红黑树的文章如同算法导论书中那样,都是上来直接给出一些分类情况,以及每个分类情况下的处理办法,而没有着重讲述为什么这么分类,为什么这个分类下执行这些操作,即只介绍了how,没有重点给出why。本篇文章的重点就在于解释why。
这样可能就导致一种现象:我按照这些分类以及分类下的操作办法,的确完整的走通想通了整个算法过程,感觉应该理解红黑树了,但是可能过了几个月后就忘记如何分类的了,忘记分类下如何操作的了。
归根到底是我们没有找出最本质的东西,比如说插入节点时遇到父子是红红的问题,对应的2个直接的解决办法如下:
- 将父节点改成黑色
- 将一个红节点扔到另一个子树中
这2个解决办法就是直接解决当前父子红红问题的,然后就可以在这2个办法的基础上进行详细的开展,就会推出插入节点时的分类情况及其操作办法了。文章的后面会详细展开这部分的推理,下面还是先把基础的二叉搜索树介绍下。
1 二叉搜索树
1.1 定义
二叉搜索树中的每个节点含有如下属性,key、left、right、p,分别对应该节点的值、左孩子、右孩子和父节点。
并且满足如下性质:
设x是二叉搜索树的一个节点,如果y是x左子树中的一个节点,那么y.keyx.key。
如下所示:
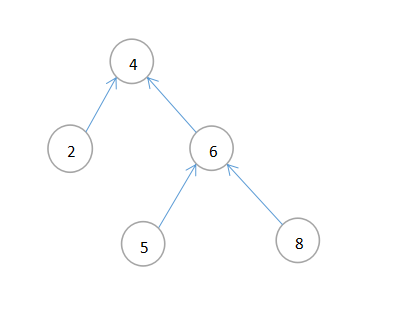
1.2 基本操作
最大、最小值都很简单,这里不再赘述了。
1.2.1 前驱和后继
按照中序遍历的方式来给出指定节点的前驱和后继
-
后继
如果该节点有右子树,则后继节点就是右子树的最小值 如果没有右子树,则后继沿着该节点往上找到一个父节点,该父节点的左子树包含当前节点。 如何来理解呢? 中序遍历的顺序为:左根右。那么以当前节点作为根,查找它的后继: 如果有右子树,则 为 (左子树)根(右子树) ,很明显紧跟根后面的就是右子树中的第一个元素,按照中序遍历的方式右子树中第一个元素就是右子树的最小值 如果没有右子树,则为 (左子树)根,该部分中序遍历结束,那么这一部分可能是上层父节点的左子树部分或者右子树部分,如果是上层父节点的右子树部分,那么上一层父节点的根在该部分的前面,即为 根1((左子树)根),此时同理,上层父节点的根也中序遍历完毕,开始上上层父节点的遍历,如果还是右子树,继续轮回,即为 根2 根1((左子树)根), 如果是左子树,那么下一个父节点则在该部分的右面,即,根2 根1((左子树)根)根3。所以我们要找的节点的后继就是根3。 最好在纸上进行划分下。该算法见算法导论中下图  -
前驱
同理
1.3 查找
也挺简单的,如下:

1.4 插入
也比较简单,就是对比找到一个节点,直到遇到NIL节点,则该NIL节点的父节点就是要插入节点的父节点
然后再判断要插入的节点是比父节点大还是小,大的话作为右节点,小的话作为左节点。
见算法导论中下图:
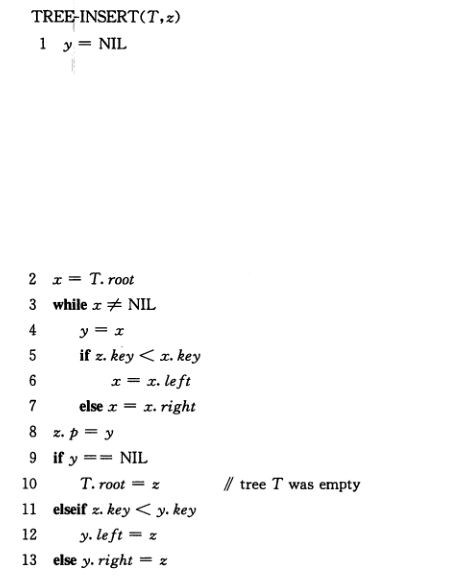
1.5 删除
针对要删除节点(设为z节点)的孩子,分下面3种情况:
- 无孩子:直接删除当前节点即可,修改父节点,用NIL作为孩子替换z。
- 只有一个孩子:修改父节点,将该孩子替换z。
-
有2个孩子:找到z的后继(这里设置为y)来替换z。此时的后继y必然是z的右子树中的最小值。这就需要先将y从右子树中摘出来,即需要先将y的右子树替换y,摘出y后,再用y去替换z。让z的左子树作为y的左子树,z的新右子树(摘除y之后)作为y的右子树。
总结下就是:y(一定没有左孩子)的右孩子替换y,y替换z的过程。 此时有一个可以优化的地方就是:如果y是z的右孩子,那么z的新右子树就是y的右子树,那么此时就可以不用摘除了。
算法内容如下:
先定义一个节点替换的方法:

整体删除逻辑如下:

至此,基础的二叉搜索树就算铺垫完成了,下面就是重点的红黑树了。
2 红黑树
2.1 红黑树的5个性质
- 1 每个节点或是红色,或是黑色
- 2 根节点是黑色
- 3 每个叶节点(NIL)是黑色
- 4 如果一个节点是红色,则它的2个子节点都是黑色
- 5 对于每个节点,从该节点到其所有后代叶节点的简单路径上,均包含相同数目的黑色节点
一颗红黑树示例如下:
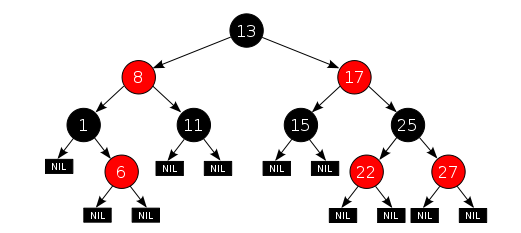
可以得出的一些结论:
-
红黑树的任何一个节点的左右子树的高度最多是另一子树的2倍。
由性质5和性质4可以得出,最短的路径都是黑色节点,最长的路径有交替的红色和黑色节点,所以一个子树最多是另一个子树高的的2倍,就是所谓的近似平衡。
2.2 旋转
可以参见下这里的一个动画浅谈算法和数据结构: 九 平衡查找树之红黑树

旋转的作用:
- 用来平衡左右子树的高度,而不违反二叉搜索树的性质,简单可以理解为将一个节点扔到另一个子树中
2.3 插入
2.3.1 普通插入
按照上述二叉搜索树的插入方式
2.3.2 插入后的修正
新插入的节点着色为红色,暂叫z节点,z的父节点叫z.p,它会违反红黑树的哪些性质?
-
违反性质2
如果插入节点是根节点,则违反了性质2。此时只需要将z节点重新着为黑色即可。 -
违反性质4
如果z.p是红色,那么就违反了性质4。下面就针对性质4来具体的分析怎么解决
目前要解决的问题是:z是红色,z.p也是红色
可以得到的一些结论:
-
z.p.p必然是黑色
因为在z插入之前是一颗红黑树,必然要满足性质4,所以z.p.p是黑色,z的叔父节点是不确定的,可红可黑。 -
z的兄弟节点只能是叶节点(黑色的)
z.p是红色的,则z的兄弟节点必须是黑色的,如果z的兄弟节点不是叶节点,则z的兄弟节点必然比z这一路多了一个黑色,不满足性质5,所以z的兄弟节点是黑色的叶节点。
解决问题的要领:
不能增加或者减少黑高,只能部分增加并且部分减少然后相互抵消
解决父子红红问题有2个思路:
- 1 把z.p变成黑色,z.p.p变成红色
- 2 把z和z.p中的一个红色节点扔到z.p.p的另一个子树中
再来详细分析下这2个思路:
-
1 把z.p由红色变成黑色,z.p.p由黑色变成红色
z这一路增加一个黑色,减少一个黑色,黑高不变。但是z的叔父那一路就会因为z.p.p而少了一个黑色,所以如果z的叔父是红色,那么可以将z的叔父由红色变成黑色来抵消z.p.p的减少。 所以这个就要求z的叔父节点是红色。 但是这并没有完,我们将z.p.p由黑色变成红色,可能又会出现父子红红的情况,所以继续下一次的轮回 初始为:  转变成如下:  -
2 把z和z.p中的一个红色扔到z.p.p的另一个子树中
这个扔的操作就是通过左旋或者右旋,目前假如是右旋,即将z.p提升为z.p.p的位置,将z.p.p拉下来作为z的叔父节点的一路。颜色上,z.p由红变成黑色,z.p.p由黑色变成红色(这就要求z的叔父必须是黑色,不然又出现红红)。此时z和z的叔父2路都没有增加或者减少黑色。同时z.p的右子树会作为z.p.p的左子树(右旋的结果),此时z.p.p是红色,则z.p的右子树必须是黑色,即z必须是z.p的左子树。 一种情况z本来就是z.p的左孩子,另一种情况z是z.p的右孩子,那么可以通过左旋就可以实现,然后减交换z和z.p的位置。所以这里又分2种情况。分析完毕,下面看图形示意。 初始为:  这里需要将4或者5中的一个红色扔到6的另一个子树中,那么执行右旋后如下:  这里其实就要求5节点必须是黑色,即在旋转前4节点的右孩子必须是黑色,那么z必须是4节点的左孩子。这里我们只需要执行下左旋,将可以将红色的子转变成红色的父的左孩子,此时再将z节点设置为红色的子即4节点即可,执行上述的操作了。 
总上2点解决方案的分析,我们可以得出如下的3个分类情况以及解决办法:
-
1 z的叔节点y是红色
即按照上述思路1中的方式,把z.p由红色变成黑色,z.p.p由黑色变成红色,z这一路保持黑高不变,z的叔节点由红色变成黑色,同样保持了黑高不变。z.p.p重新定义为z,继续下一次的轮回。 -
2 z的叔节点y是黑色的且z是一个右孩子
即按照上述思路2中的方式,通过左旋,来保证z.p的右子树不能是红色,必须是黑色(因为这个右子树将来要作为红色节点的孩子节点) -
3 z的叔节点y是黑色的且z是一个左孩子
即按照上述思路2中的方式,通过对z.p进行右旋,z.p顶替了z.p.p及其颜色,z.p.p拉下着为红色,并将z.p之前的右子树挂到z.p.p的左子树下。
2.4 删除
2.4.1 普通删除
再来简单回顾下二叉搜索树的删除:
要删除的节点为z
删除就是分如下的3个条件:
- z没有孩子:直接删除
- z只有1个孩子:将孩子替换z
- z有2个孩子:用z的后继y来替换z,同时y的右孩子来替换y的过程。
2.4.2 修正
这时候可能有3个节点:
- z:要删除的节点
- y:z的后继
- r:y的右孩子
在没删除之前,要删除的节点z的颜色可红可黑,y可红可黑,r如果存在的话只能是红色(因为y是没有左孩子的,如果r存在并且是黑色的,那么r这一路包含的黑色节点个数比y的另一路多,不符合性质5)。
问题就来了:这里有几个位置的节点需要进行修复?z的位置?y的位置?r的位置?
结合上面删除的3种情况来详细分析下:
-
z没有孩子:直接删除。
如果z是红色的话,此时什么性质都没有违反。 如果z是黑色的话,那么就少了一个黑色,之后需要补一个黑色。 -
z只有一个孩子:直接将孩子替换成z。
如果z是红色,则z的孩子必然都是黑色,由于只有1个孩子,那么就违反了性质5,则这种情况是不存在的。 那么z只能是黑色,并且那一个孩子只能是红色。此时孩子替换了z,缺少了一个黑色,需要补回来。 -
z有2个孩子:y的右孩子替换y(如果有的话),y替换z
那么z的后继y要替换z,继承z的颜色,那么z处就仍保持不变。y的右孩子r(如果有的话)要替换y,那么此时可能违反性质的地方就是y处了。 如果y是红色,则孩子必须是黑色,y是z的后继,则y是没有左孩子,y如果有右孩子,则必然是黑色,此时又不满足性质5。所以y是红色的时候,y是没有右孩子的。那么此时删除y就不违反任何性质。 如果y是黑色,如果有右孩子,则必然是红色(如果是黑色则不满足性质5)。所以不管有没有右孩子,此时删除y都是少了个黑色的,需要补回来的。
从上面可以看到有时候是需要修复z处的,有时候是需要修复y处的。进行统一概括的话,设置一个变量为x节点,该节点为需要修复的地方,得到如下结论:
- 如果x处节点原本是红色的话,没有违反任何性质,不需要修复
- 如果x处节点原本是黑色的话,都是少了一个黑色,需要修复的
其中x在前2种情况下就是原z处节点,在最后一种情况下就是原y处节点。
下面要解决的问题就是:对x节点缺少一个黑色的修复
最直接的解决办法如下:
- 1 对x这一路多补充一个黑色节点,即执行一次左旋或者右旋,往x这一路多扔一个节点,然后将该节点着为黑色
- 2 对x的父节点加一层黑色
下面就来详细展开下上述2个解决办法,来推导出对应的情况:
-
1 对x这一路多补充一个黑色节点,即执行一次左旋或者右旋,往x这一路多扔一个节点,然后将该节点着为黑色
这时候相当于x的兄弟节点那一路要给出一个节点,即它就少了一个节点。少了一个节点还要能保住黑高不变,则必然是扔了一个红色节点过来。扔过来后,再把该节点着为黑色,就为x这一路多增加了一个黑色,从而弥补了缺少的黑色。
设定x的兄弟节点是w。上述扔的操作可能执行的是左旋也可能是右旋,这里先假定是左旋。则这里w的右孩子替代w,w替代w的父节点及其颜色,w的父节点拉下来,并着为黑色。
根据上述描述,要想保证w这一路在少了一个节点之后,黑色数目不变,则w和w的右孩子必然有一个是红色,一个是黑色(2红违反性质4所以不可能,2黑则必然要少一个黑色所以也不可能)。到底谁是红色呢?
w的左孩子要作为w的原来父节点(该节点要被着为黑色)的右孩子,所以w的左孩子要挂在黑色的父节点下,要想保证黑高不变,那么该节点之前挂在w节点下,那么w节点也必须是黑色,则w的右孩子是红色了。
下面来看下这个过程:
原本为:
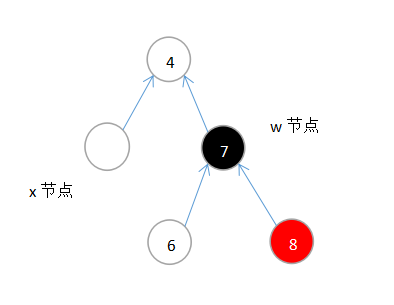
经过上述左旋并着色的操作过程后为:
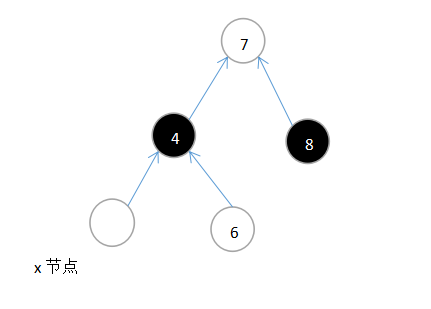
所以只要满足了w为黑色,w的右孩子为红色,就可以采用该解决办法
为了满足w为黑色,w的右孩子为红色。也分如下几种情况:
- w为红色,则w的孩子必然为黑色(你可能认为万一w没有孩子怎么办?这里是不可能的,因为w的另一路z缺少了一个黑色,那么之前必然有一个黑色,而如果w没有孩子,则w这一路必然比z那一路少一个黑色,不满足性质5,所以不存在这种可能)。这时候如果对w进行左旋或者是右旋必然会改变左右黑高的不平衡。w为红色,则w.p为黑色,此时可以把w这一路的红色扔过去即执行左旋,w.p变为红色,w变为黑色。w的左子树(左孩子为黑色)作为w.p的右孩子。重新更正w为原w的左孩子,由于颜色为黑色,则可转到如下几种情况:
- w为黑色,w的右孩子为红色,这种本身就满足
- w为黑色,w的右孩子为黑色,左孩子为黑色:这种不存在红色,排除
-
w为黑色,w的右孩子为黑色,左孩子为红色:可以进行右旋,如下图所示的转换
原本为:  右旋并着色后: 
- 2 对x的父节点加一个黑色
父节点加一个黑色,那么就要求x的兄弟节点必须要减少一个黑色。从上述解决办法1种可以得到,只有在w为黑色,w的2个孩子都为黑色的时候,无法采用解决办法1。这时候可以来采用解决办法2。
将w着为红色,那么w这一路就可以减少一个黑色。
减少了一个黑色之后,如果x的父节点是红色,那么直接将红色着为黑色,即可达到父节点多加一个黑色。如果x的父节点是黑色,那么就意味着x的父节点无法增加一个黑色,即缺少一个黑色,即将x设置为x的父节点,重新进入下一个轮回。
你可能意识到,如果一直轮回直到x的父节点是根,此时仍无法添加一个黑色,那么此时相当于全部所有节点都减少了一个黑色,仍然是不违反任何性质的,只是比之前的黑高小1。
所以从上面的2个解决办法中可以总结出来如下算法导论中的4种情况:
-
1 x的兄弟节点w是红色:
可以通过左旋来重新更正w的位置,更正后的w为黑色,转为如下几种情况 -
2 x的兄弟节点w是黑色,w的孩子全部是黑色
利用解决办法2,将x的父节点加一个黑色,将w这一路减少一个黑色。如果父节点是红色,那么直接着为黑色即相当于加上了黑色,如果父节点是黑色,那么将x设置为x的父节点,认为此时x仍然是缺少一个黑色,即开始下一个轮回 -
3 x的兄弟节点w是黑色,w的右孩子是黑色,左孩子是红色:
可以通过右旋达到下面的情况4 -
4 x的兄弟节点w是黑色,w的右孩子是红色
可以利用解决办法1,将w那一路的红色节点扔到x这一路,然后着为黑色,即x增加了一个黑色。而w那一路减少的是一个红色,所以黑高仍然保持不变。
至此,我们来总结下删除的2个重要过程:
-
1 确定要修复的x的位置
x的位置可能是z处,也可能是y处。参见算法导论中这一个过程:  上述RB-TRANSPLANT函数就是节点替换的函数,RB-DELETE-FIXUP函数就是修正函数 -
2 修正过程
修正过程即按照上述的分析总结对应的4种情况来处理,见算法导论如下图 
至此,总算是将红黑树主要的插入和删除描述完毕了。
3 红黑树总结
过程各种分析情况挺多的,但是我们更应该去记住本质的东西,从而能够达到自己去推理对应的过程,所以再次强调
-
插入:
为了解决父子红红问题,有如下2种直接的解决办法:
- 父节点设置为黑色
- 一个红节点扔到另一个子树中
-
删除:
为了解决缺少一个黑色的问题,有如下2种直接的解决办法:
- 增加一个黑色节点,可以通过左旋来得到,即另一子树扔过来一个红色(本身保证黑色不减少)
- 父节点增加一个黑色
我们从上述直接的解决办法中就可以推理出去,自然就能得到该怎么分类,每个分类下具体怎么操作了。
一个可以检验你是否真的理解红黑树的办法就是:不借助任何东西,你自己是否能够在一张白纸上自己推导一遍。
本文章涉及到细节很多,难免有疏漏的地方,还请批评指正。
欢迎继续来讨论,越辩越清晰。
欢迎关注微信公众号:乒乓狂魔