动态规划法（一）从斐波那契数列谈起

动态规划法与分治方法

  动态规划（Dynamic Programming）与分治方法相似，都是通过组合子问题的解来求解原问题。不同的是，分治方法通常将问题划分为互不相交的子问题，递归地求解子问题，再讲它们的解组合起来，求出原问题的解。而动态规划应用于子问题重叠的情况，即不用的子问题具有公共的子子问题。在这种情况下，如果采用分治算法，则分治算法会做许多不必要的工作，它会反复地求解那些公共子子问题。对于动态规划法，它对每个子子问题只求解一次，将其保存在一个表格中，从而无需每次求解一个子子问题时都重新计算，避免了这种不必要的计算工作。
  也就是说，动态规划法与分治方法相比，是用空间来换时间，而时间上获得的效益是很客观的，这是一种典型的时空平衡（time-memory trade-off）的策略。通常，动态规划法用来求解最优化问题（optimization problem），如斐波那契数列求值问题，钢条切割问题，0-1背包问题，矩阵链乘法问题，最长公共子序列（LCS）问题，最优二叉搜索树问题等。
  一般情况下，动态规划算法的步骤如下：

1. 刻画一个最优解的结构特征。
2. 递归地定义最优解的值。
3. 计算最优解的值，通常采用自底向上的方法。
4. 利用计算出的信息构造一个最优解。

  接下来，我们将从斐波那契数列求值这个简单的例子入手，来分析动态规划法的具体步骤和优点。

斐波那契数列

  斐波那契数列记为{f(n)}{f(n)}，其表达式如下：

  具体写出前几项，就是：0,1,1,2,3,5,8,13,21,34,55,89,144,233……
  接下来，我们将会采用递归法和动态规划法来求解该数列的第n项，即f(n)的值。

递归法求解

  首先，我们采用递归法来求解斐波那契数列的第n项f(n)f(n),其算法描述如下：

function fib(n)
    if n = 0 return 0
    if n = 1 return 1
    return fib(n − 1) + fib(n − 2)

分析上述伪代码，先是定义一个函数fib(n),用来计算斐波那契数列的第n项，当n≥2n≥2时，它的返回值会调用函数fib(n-1)和fib(n-2).当n=5n=5时，计算fib(5)的函数调用情况如下图所示：

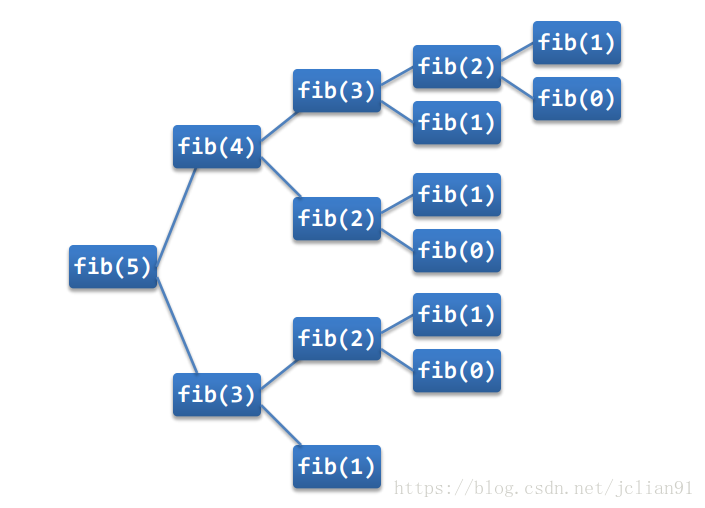
在计算fib(5)时，fib(5)调用1次，fib(4)调用1次，fib(3)调用2次，fib(2)调用3次，fib(1)调用5次，fib(0)调用3次，一共调用函数fib()15次。由此，我们可以看到，在计算fib(5)时，存在多次重复的fib()函数的调用，当n增大时，重复调用的次数会急剧增加，如计算fib(50)时，fib(1)和fib(0)大约会被调用 2.4×10102.4×1010次。由此可见，该算法的效率并不是很高，因为该算法的运行时间是指数时间。
  我们用Python实现上述算法，并计算f(38)的值及运算时间。Python代码如下：

import time

# recursive method
def rec_fib(n):
    if n <= 1:
        return n
    else:
         return rec_fib(n-1) + rec_fib(n-2)

# time cost of cursive method
t1 = time.time()
t = rec_fib(38)
t2 = time.time()

print('结果：%s, 运行时间：%s'%(t, t2-t1))

输出结果如下：

结果：39088169, 运行时间：22.93831205368042

动态规划法求解

  在使用递归法来求解斐波那契数列的第n项时，我们看到了递归法的不足之处，因为递归法在使用过程中存在大量重复的函数调用，因此，效率很差，运行时间为指数时间。为了解决递归法存在的问题，我们可以尝试动态规划法，因为动态规划法会在运行过程中，保存上一个子问题的解，从而避免了重复求解子问题。对于求解斐波那契数列的第n项，我们在使用动态规划法时，需要保存f(n-1)和f(n-2)的值，牺牲一点内存，但是可以显著地提升运行效率。
  动态规划法来求解斐波那契数列第n项的伪代码如下：

function fib(n)

    var previousFib := 0, currentFib := 1

    if n = 0
    return 0
    else if n = 1
    return 1

    repeat n−1 times
        var newFib := previousFib + currentFib
        previousFib := currentFib
        currentFib := newFib

    return currentFib

在上述伪代码中，并没有存在重复求解问题，只是在每次运行过程中，保存上两项的值，再利用公式f(n)=f(n−1)+f(n−2)f(n)=f(n−1)+f(n−2)来求解第n项的值。用Python实现上述过程，代码如下：

import time

# bottom up approach of Dynamic Programming
def dp_fib(n):
    previousFib = 0
    currentFib = 1
    if n <= 1:
        return n

    # repeat n-1 times
    for _ in range(n-1):
        newFib = previousFib + currentFib
        previousFib = currentFib
        currentFib = newFib

    return currentFib

# time cost of DP method
t1 = time.time()
t = dp_fib(38)
t2 = time.time()

print('结果：%s, 运行时间：%s'%(t, t2-t1))

输出结果如下：

结果：39088169, 运行时间：0.0

  显然，使用动态规划法来求解斐波那契数列第n项的运行效率是很高的，因为，该算法的时间复杂度为多项式时间。

参考文献

1. 算法导论（第四版）
2. https://www.cs.upc.edu/~jordicf/Teaching/programming/pdf/IP07_Recursion.pdf
3. https://www.saylor.org/site/wp-content/uploads/2011/06/Dynamic-Programming.pdf

附录

用递归法和动态规划法来求解该数列的第n项，完整的Python代码如下：

# calculate nth item of Fibonacci Sequence
import time

# recursive method
def rec_fib(n):
    if n <= 1:
        return n
    else:
         return rec_fib(n-1) + rec_fib(n-2)

# bottom up approach of Dynamic Programming
def dp_fib(n):
    previousFib = 0
    currentFib = 1
    if n <= 1:
        return n

    # repeat n-1 times
    for _ in range(n-1):
        newFib = previousFib + currentFib
        previousFib = currentFib
        currentFib = newFib

    return currentFib

 # time cost of cursive method
t1 = time.time()
t = rec_fib(38)
t2 = time.time()
print('结果：%s, 运行时间：%s'%(t, t2-t1))
# time cose of DP method
s = dp_fib(38)
t3 = time.time()
print('结果：%s, 运行时间：%s'%(t, t3-t2))

输出结果如下：

结果：39088169, 运行时间：22.42628264427185
结果：39088169, 运行时间：0.0

完整的Java代码如下：

package DP_example;

import java.util.Date;
import java.math.BigInteger;

public class fib {
    // 主函数
    public static void main(String[] args) {
        Date start_time =  new Date(); //开始时间
        int n = 38;
        BigInteger t1 = DP_fib(n);  // 动态规划法求解
        Date end_time1 =  new Date(); // 结束时间
        Long cost_time1 = end_time1.getTime()-start_time.getTime();  // 计算时间，返回毫秒数
        System.out.println(String.format("The fib(%d) is %s.\nCost time is %.3fs.", n, t1, cost_time1*1.0/1000));


        BigInteger t2 = rec_fib(n);  // 递归法求解
        Date end_time2 =  new Date(); // 结束时间
        Long cost_time2 = end_time2.getTime()-end_time1.getTime();  // 计算时间，返回毫秒数
        System.out.println(String.format("The fib(%d) is %s.\nCost time is %.3fs.", n, t2, cost_time2*1.0/1000));

    }

    // 利用递归方法计算斐波那契数列的第n项
    public static BigInteger rec_fib(int n){
        if(n == 0)
            return BigInteger.ZERO;
        if(n ==1)
            return BigInteger.ONE;
        else
            return rec_fib(n-1).add(rec_fib(n-2));
    }

    // 利用动态规划法(DP)计算斐波那契数列的第n项
    public static BigInteger DP_fib(int n){
        if(n == 0)
            return BigInteger.ZERO;
        if(n == 1)
            return BigInteger.ONE;
        else {
            BigInteger previousFib = BigInteger.ZERO;
            BigInteger currentFib = BigInteger.ONE;
            BigInteger newFib;

            for(int i=1; i<n; i++){ // 重复循环n-1次
                newFib =  previousFib.add(currentFib);
                previousFib = currentFib;
                currentFib = newFib;
            }

            return currentFib;
        }
    }
}

输出结果如下所示：

The fib(38) is 39088169.
Cost time is 0.001s.
The fib(38) is 39088169.
Cost time is 2.172s.