字符串匹配问题的形式定义:
- 文本(Text)是一个长度为 n 的数组 T[1..n];
- 模式(Pattern)是一个长度为 m 且 m≤n 的数组 P[1..m];
- T 和 P 中的元素都属于有限的字母表 Σ 表;
- 如果 0≤s≤n-m,并且 T[s+1..s+m] = P[1..m],即对 1≤j≤m,有 T[s+j] = P[j],则说模式 P 在文本 T 中出现且位移为 s,且称 s 是一个有效位移(Valid Shift)。

比如上图中,目标是找出所有在文本 T = abcabaabcabac 中模式 P = abaa 的所有出现。该模式在此文本中仅出现一次,即在位移 s = 3 处,位移 s = 3 是有效位移。
解决字符串匹配的算法包括:朴素算法(Naive Algorithm)、Rabin-Karp 算法、有限自动机算法(Finite Automation)、 Knuth-Morris-Pratt 算法(即 KMP Algorithm)、Boyer-Moore 算法、Simon 算法、Colussi 算法、Galil-Giancarlo 算法、Apostolico-Crochemore 算法、Horspool 算法、Shift-Or 算法和 Sunday 算法等。本文中我们将主要介绍 Boyer-Moore 算法(即 BM Algorithm)。
在 1977 年,Robert S. Boyer (Stanford Research Institute) 和 J Strother Moore (Xerox Palo Alto Research Center) 共同发表了文章《A Fast String Searching Algorithm》,介绍了一种新的快速字符串匹配算法。这种算法在逻辑上相对于现有的算法有了显著的改进,它对要搜索的字符串进行倒序的字符比较,并且当字符比较不匹配时无需对整个模式串再进行搜索。
Boyer-Moore 算法的主要特点有:
- 对模式字符的比较顺序时从右向左;
- 预处理需要 O(m + σ) 的时间和空间复杂度;
- 匹配阶段需要 O(m × n) 的时间复杂度;
- 匹配阶段在最坏情况下需要 3n 次字符比较;
- 最优复杂度 O(n/m);
下面是几种常见的字符串匹配算法的性能比较。
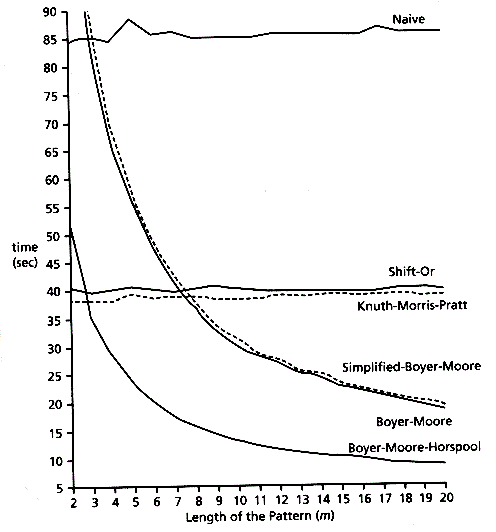
在 Naive 算法中,对文本 T 和模式 P 字符串均未做预处理。而在 KMP 算法中则对模式 P 字符串进行了预处理操作,以预先计算模式串中各位置的最长相同前后缀长度的数组。Boyer–Moore 算法同样也是对模式 P 字符串进行预处理。
我们知道,在 Naive 算法中,如果发现模式 P 中的字符与文本 T 中的字符不匹配时,需要将文本 T 的比较位置向后滑动一位,模式 P 的比较位置归 0 并从头开始比较。而 KMP 算法则是根据预处理的结果进行判断以使模式 P 的比较位置可以向后滑动多个位置。Boyer–Moore 算法的预处理过程也是为了达到相同效果。
Boyer–Moore 算法在对模式 P 字符串进行预处理时,将采用两种不同的启发式方法。这两种启发式的预处理方法称为:
- 坏字符(Bad Character Heuristic):当文本 T 中的某个字符跟模式 P 的某个字符不匹配时,我们称文本 T 中的这个失配字符为坏字符。
- 好后缀(Good Suffix Heuristic):当文本 T 中的某个字符跟模式 P 的某个字符不匹配时,我们称文本 T 中的已经匹配的字符串为好后缀。
Boyer–Moore 算法在预处理时,将为两种不同的启发法结果创建不同的数组,分别称为 Bad-Character-Shift(or The Occurrence Shift)和 Good-Suffix-Shift(or Matching Shift)。当进行字符匹配时,如果发现模式 P 中的字符与文本 T 中的字符不匹配时,将比较两种不同启发法所建议的移动位移长度,选择最大的一个值来对模式 P 的比较位置进行滑动。
此外,Naive 算法和 KMP 算法对模式 P 的比较方向是从前向后比较,而 Boyer–Moore 算法的设计则是从后向前比较,即从尾部向头部方向进行比较。
下面,我们将以 J Strother Moore 提供的例子作为示例。
Text T : HERE IS A SIMPLE EXAMPLE
Pattern P : EXAMPLE
首先将文本 T 与模式 P 头部对齐,并从尾部开始进行比较。(注1)

这样如果尾部的字符不匹配,则前面的字符也就无需比较了,直接跳过。我们看到,"S" 与 "E" 不匹配,我们称文本 T 中的失配字符 "S" 为坏字符(Bad Character)。
由于字符 "S" 在模式 "EXAMPLE" 中不存在,则可将搜索位置滑动到 "S" 的后面。

仍然从尾部开始比较,发现 "P" 与 "E" 不匹配,所以 "P" 是坏字符。但此时,"P" 包含在模式 "EXAMPLE" 之中。所以,将模式后移两位,使两个 "P" 对齐。

由此总结坏字符启发法的规则是:
模式后移位数 = 坏字符在模式中失配的位置 - 坏字符在模式中最后一次出现的位置
坏字符启发法规则中的特殊情况:
- 如果坏字符不存在于模式中,则最后一次出现的位置为 -1。
- 如果坏字符在模式中的位置位于失配位置的右侧,则此启发法不提供任何建议。
The bad character shift means to shift the pattern so that the text character of the mismatch is aligned to the last occurrence of that character in the initial part of the pattern (pattern minus last pattern character), if there is such an occurrence, or one position before the pattern if the mismatched character doesn't appear in the initial part of the pattern at all.
以上面示例中坏字符 "P" 为例,它的失配位置为 "E" 的位置 6 (位置从 0 开始),在模式中最后一次出现的位置是 4,则模式后移位数为 6 - 4 = 2 位。模式移动的结果就是使模式中最后出现的 "P" 与文本中的坏字符 "P" 进行对齐。
实际上,前面的坏字符 "S" 出现时,其失配位置为 6,最后一次出现位置为 -1,所以模式后移位数为 6 - (-1) = 7 位。也就是将模式整体移过坏字符。
我们继续上面的过程,仍然从尾部开始比较。

仍然从尾部开始比较,发现 "E" 与 "E" 匹配,则继续倒序比较。

发现 "L" 与 "L" 匹配,则继续倒序比较。

发现 "P" 与 "P" 匹配,则继续倒序比较。

发现 "M" 与 "M" 匹配,则继续倒序比较。

发现 "I" 与 "A" 不匹配,则 "I" 是坏字符。对于前面已经匹配的字符串 "MPLE"、"PLE"、"LE"、"E",我们称它们为好后缀(Good Suffix)。
The good suffix shift, aligns the matched part of the text with the rightmost occurrence of that character sequence in the pattern that is preceded by a different character (including none, if the matched suffix is also a prefix of the pattern) than the matched suffix of the pattern - if there is such an occurrence.
而好后缀启发法的规则是:
模式后移位数 = 好后缀在模式中的当前位置 - 好后缀在模式中最右出现且前缀字符不同的位置
好后缀在模式中的当前位置以其最后一个字符为准。如果好后缀不存在于模式中,则最右出现的位置为 -1。
这样,我们先来找出好后缀在模式中上一次出现的位置。
- "MPLE" : 未出现,最右出现的位置为 -1;
- "PLE" : 未出现在头部,最右出现的位置为 -1;
- "LE" : 未出现在头部,最右出现的位置为 -1;
- "E" : 出现在头部,补充虚拟字符 'MPL'E,前缀字符为空,最右出现的位置为 0;
由于只有 "E" 在模式中出现,其当前位置为 6,上一次出现的位置为 0,则依据好后缀启发法规则,模式后移位数为 6 - 0 = 6 位。
而如果依据坏字符启发法规则,模式后移位数为 2 - (-1) = 3 位。
Boyer–Moore 算法的特点就在于此,选择上述两种启发法规则计算结果中最大的一个值来对模式 P 的比较位置进行滑动。这里将选择好后缀启发法的计算结果,即将模式向后移 6 位。

此时,仍然从尾部开始比较。

发现 "P" 与 "E" 不匹配,则 "P" 是坏字符,则模式后移位数为 6 - 4 = 2 位。

发现 "E" 与 "E" 匹配,则继续倒序比较,直到发现全部匹配,则匹配到的第一个完整的模式 P 被发现。
继续下去则是依据好后缀启示法规则计算好后缀 "E" 的后移位置为 6 - 0 = 6 位,然后继续倒序比较时发现已超出文本 T 的范围,搜索结束。
从上面的示例描述可以看出,Boyer–Moore 算法的精妙之处在于,其通过两种启示规则来计算后移位数,且其计算过程只与模式 P 有关,而与文本 T 无关。因此,在对模式 P 进行预处理时,可预先生成 "坏字符规则之向后位移表" 和 "好后缀规则之向后位移表",在具体匹配时仅需查表比较两者中最大的位移即可。
下面是 Boyer–Moore 算法的示例代码,使用 C# 语言实现。
1 namespace StringMatching 2 { 3 class Program 4 { 5 static void Main(string[] args) 6 { 7 char[] text1 = "BBC ABCDAB ABCDABCDABDE".ToCharArray(); 8 char[] pattern1 = "ABCDABD".ToCharArray(); 9 10 int firstShift1; 11 bool isMatched1 = BoyerMooreStringMatcher.TryMatch( 12 text1, pattern1, out firstShift1); 13 Contract.Assert(isMatched1); 14 Contract.Assert(firstShift1 == 15); 15 16 char[] text2 = "ABABDAAAACAAAABCABAB".ToCharArray(); 17 char[] pattern2 = "AAACAAAA".ToCharArray(); 18 19 int firstShift2; 20 bool isMatched2 = BoyerMooreStringMatcher.TryMatch( 21 text2, pattern2, out firstShift2); 22 Contract.Assert(isMatched2); 23 Contract.Assert(firstShift2 == 6); 24 25 char[] text3 = "ABAAACAAAAAACAAAABCABAAAACAAAAFDLAAACAAAAAACAAAA" 26 .ToCharArray(); 27 char[] pattern3 = "AAACAAAA".ToCharArray(); 28 29 int[] shiftIndexes3 = BoyerMooreStringMatcher.MatchAll(text3, pattern3); 30 Contract.Assert(shiftIndexes3.Length == 5); 31 Contract.Assert(string.Join(",", shiftIndexes3) == "2,9,22,33,40"); 32 33 char[] text4 = "GCATCGCAGAGAGTATACAGTACG".ToCharArray(); 34 char[] pattern4 = "GCAGAGAG".ToCharArray(); 35 36 int firstShift4; 37 bool isMatched4 = BoyerMooreStringMatcher.TryMatch( 38 text4, pattern4, out firstShift4); 39 Contract.Assert(isMatched4); 40 Contract.Assert(firstShift4 == 5); 41 42 char[] text5 = "HERE IS A SIMPLE EXAMPLE AND EXAMPLE OF BM.".ToCharArray(); 43 char[] pattern5 = "EXAMPLE".ToCharArray(); 44 45 int firstShift5; 46 bool isMatched5 = BoyerMooreStringMatcher.TryMatch( 47 text5, pattern5, out firstShift5); 48 Contract.Assert(isMatched5); 49 Contract.Assert(firstShift5 == 17); 50 int[] shiftIndexes5 = BoyerMooreStringMatcher.MatchAll(text5, pattern5); 51 Contract.Assert(shiftIndexes5.Length == 2); 52 Contract.Assert(string.Join(",", shiftIndexes5) == "17,29"); 53 54 Console.WriteLine("Well done!"); 55 Console.ReadKey(); 56 } 57 } 58 59 public class BoyerMooreStringMatcher 60 { 61 private static int AlphabetSize = 256; 62 63 private static int Max(int a, int b) { return (a > b) ? a : b; } 64 65 static int[] PreprocessToBuildBadCharactorHeuristic(char[] pattern) 66 { 67 int m = pattern.Length; 68 int[] badCharactorShifts = new int[AlphabetSize]; 69 70 for (int i = 0; i < AlphabetSize; i++) 71 { 72 //badCharactorShifts[i] = -1; 73 badCharactorShifts[i] = m; 74 } 75 76 // fill the actual value of last occurrence of a character 77 for (int i = 0; i < m; i++) 78 { 79 //badCharactorShifts[(int)pattern[i]] = i; 80 badCharactorShifts[(int)pattern[i]] = m - 1 - i; 81 } 82 83 return badCharactorShifts; 84 } 85 86 static int[] PreprocessToBuildGoodSuffixHeuristic(char[] pattern) 87 { 88 int m = pattern.Length; 89 int[] goodSuffixShifts = new int[m]; 90 int[] suffixLengthArray = GetSuffixLengthArray(pattern); 91 92 for (int i = 0; i < m; ++i) 93 { 94 goodSuffixShifts[i] = m; 95 } 96 97 int j = 0; 98 for (int i = m - 1; i >= -1; --i) 99 { 100 if (i == -1 || suffixLengthArray[i] == i + 1) 101 { 102 for (; j < m - 1 - i; ++j) 103 { 104 if (goodSuffixShifts[j] == m) 105 { 106 goodSuffixShifts[j] = m - 1 - i; 107 } 108 } 109 } 110 } 111 112 for (int i = 0; i < m - 1; ++i) 113 { 114 goodSuffixShifts[m - 1 - suffixLengthArray[i]] = m - 1 - i; 115 } 116 117 return goodSuffixShifts; 118 } 119 120 static int[] GetSuffixLengthArray(char[] pattern) 121 { 122 int m = pattern.Length; 123 int[] suffixLengthArray = new int[m]; 124 125 int f = 0, g = 0, i = 0; 126 127 suffixLengthArray[m - 1] = m; 128 129 g = m - 1; 130 for (i = m - 2; i >= 0; --i) 131 { 132 if (i > g && suffixLengthArray[i + m - 1 - f] < i - g) 133 { 134 suffixLengthArray[i] = suffixLengthArray[i + m - 1 - f]; 135 } 136 else 137 { 138 if (i < g) 139 { 140 g = i; 141 } 142 f = i; 143 144 // find different preceded character suffix 145 while (g >= 0 && pattern[g] == pattern[g + m - 1 - f]) 146 { 147 --g; 148 } 149 suffixLengthArray[i] = f - g; 150 } 151 } 152 153 return suffixLengthArray; 154 } 155 156 public static bool TryMatch(char[] text, char[] pattern, out int firstShift) 157 { 158 firstShift = -1; 159 int n = text.Length; 160 int m = pattern.Length; 161 int s = 0; // s is shift of the pattern with respect to text 162 int j = 0; 163 164 // fill the bad character and good suffix array by preprocessing 165 int[] badCharShifts = PreprocessToBuildBadCharactorHeuristic(pattern); 166 int[] goodSuffixShifts = PreprocessToBuildGoodSuffixHeuristic(pattern); 167 168 while (s <= (n - m)) 169 { 170 // starts matching from the last character of the pattern 171 j = m - 1; 172 173 // keep reducing index j of pattern while characters of 174 // pattern and text are matching at this shift s 175 while (j >= 0 && pattern[j] == text[s + j]) 176 { 177 j--; 178 } 179 180 // if the pattern is present at current shift, then index j 181 // will become -1 after the above loop 182 if (j < 0) 183 { 184 firstShift = s; 185 return true; 186 } 187 else 188 { 189 // shift the pattern so that the bad character in text 190 // aligns with the last occurrence of it in pattern. the 191 // max function is used to make sure that we get a positive 192 // shift. We may get a negative shift if the last occurrence 193 // of bad character in pattern is on the right side of the 194 // current character. 195 //s += Max(1, j - badCharShifts[(int)text[s + j]]); 196 // now, compare bad char shift and good suffix shift to find best 197 s += Max(goodSuffixShifts[j], badCharShifts[(int)text[s + j]] - (m - 1) + j); 198 } 199 } 200 201 return false; 202 } 203 204 public static int[] MatchAll(char[] text, char[] pattern) 205 { 206 int n = text.Length; 207 int m = pattern.Length; 208 int s = 0; // s is shift of the pattern with respect to text 209 int j = 0; 210 int[] shiftIndexes = new int[n - m + 1]; 211 int c = 0; 212 213 // fill the bad character and good suffix array by preprocessing 214 int[] badCharShifts = PreprocessToBuildBadCharactorHeuristic(pattern); 215 int[] goodSuffixShifts = PreprocessToBuildGoodSuffixHeuristic(pattern); 216 217 while (s <= (n - m)) 218 { 219 // starts matching from the last character of the pattern 220 j = m - 1; 221 222 // keep reducing index j of pattern while characters of 223 // pattern and text are matching at this shift s 224 while (j >= 0 && pattern[j] == text[s + j]) 225 { 226 j--; 227 } 228 229 // if the pattern is present at current shift, then index j 230 // will become -1 after the above loop 231 if (j < 0) 232 { 233 shiftIndexes[c] = s; 234 c++; 235 236 // shift the pattern so that the next character in text 237 // aligns with the last occurrence of it in pattern. 238 // the condition s+m < n is necessary for the case when 239 // pattern occurs at the end of text 240 //s += (s + m < n) ? m - badCharShifts[(int)text[s + m]] : 1; 241 s += goodSuffixShifts[0]; 242 } 243 else 244 { 245 // shift the pattern so that the bad character in text 246 // aligns with the last occurrence of it in pattern. the 247 // max function is used to make sure that we get a positive 248 // shift. We may get a negative shift if the last occurrence 249 // of bad character in pattern is on the right side of the 250 // current character. 251 //s += Max(1, j - badCharShifts[(int)text[s + j]]); 252 // now, compare bad char shift and good suffix shift to find best 253 s += Max(goodSuffixShifts[j], badCharShifts[(int)text[s + j]] - (m - 1) + j); 254 } 255 } 256 257 int[] shifts = new int[c]; 258 for (int y = 0; y < c; y++) 259 { 260 shifts[y] = shiftIndexes[y]; 261 } 262 263 return shifts; 264 } 265 } 266 }
参考资料
- Fast String Searching Algorithm Example
- Boyer–Moore string search algorithm
- Pattern Searching | Set 7 (Boyer Moore Algorithm – Bad Character Heuristic)
- The Boyer-Moore-Horspool Algorithm
- 字符串匹配的Boyer-Moore算法
- Boyer-Moore algorithm
- What are the shift rules for Boyer–Moore string search algorithm?
- CS 312 Lecture 27 - String matching
- Boyer-Moore good-suffix heuristics
- Boyer Moore Exact Pattern Matching Algorithms
注1:文章中部分示例图片来自阮一峰的博客文章《字符串匹配的Boyer-Moore算法》,这篇文章已经写的足够透彻了,但是我还是希望通过自己叙述的理解来加深记忆。
注2:本文《Boyer-Moore 字符串匹配算法》由 Dennis Gao 发表自博客园博客,任何未经作者本人允许的人为或爬虫转载均为耍流氓。
本文转自匠心十年博客园博客,原文链接:http://www.cnblogs.com/gaochundong/p/boyer_moore_string_matching_algorithm.html,如需转载请自行联系原作者




